The Graph Data Structure
Overview
Graphs come in many forms, all of which share the following properties:
- A graph is made up of two sets called the vertices and edges.
- The vertices of a graph are typed. The set may be finite or infinite.
- Not all vertices are necessarily connected by an edge; these outliers are aptly named ‘islands’.
- Each element of the edge set is a pair consisting of two elements from the vertices set.
- Edges may or may not be completely connected to every vertex.
- Edges can have weights and a direction, though neither is required.
When to Use Graphs
- When establishing ‘many-to-many’ relationships.
- i.e. more than one-to-one.
- When direction is important.
- When neighbors are important.
- When order is important.
- When the relationship between objects resembles family trees.
- When dealing with maps.
Types of Graphs
- Undirected Graphs: E(1,2) == E(2,1)
- When traversing these graphs, you do NOT have to keep direction in mind.
- Directed Graphs: E(1,2) != E(2,1)
- There is a direction that must be respected when traversing this graph.
- Vertex Labeled Graphs
- There is an order that must be followed when traversing these graphs.
- Cyclic Graph
- There is at least one cycle (i.e. return to the previous node) in this graph (hence the name).
- Edge-labeled Graphs
- There is a notion of labeling edges that has meaning.
- Weighted Graphs
- Edges have weights in this type of graph.
- Directed-Cyclic Graphs
- In addition to there being at least one cycle in this graph, there is a direction that must be followed.
- Disconnected Graphs
- This type of graph allows for islands (vertices that are not connected by an edge).
Graph Representations
- Adjacency List: an array of lists, each of which contain all the vertices that are adjacent to vertex i1.
- Adjacency Matrix: a square matrix whose elements indicate whether pairs of vertices are adjacent or not2.
- Incidence Matrix: a matrix with a row for each vertex and a column for each edge3. 1’s indicate a connection between the vertex and edge.
Graph Traversal
- Depth-first Search (DFS): Visit child vertices before sibling vertices (i.e. start from the bottom of the graph)
- In a tree, DFS can be visualized by starting at the leaves of a tree and moving up to the mother node once all leaves have been visited
- Breadth-first Search (BFS): Visit sibling vertices before child vertices
- Useful for finding the shortest path between two vertices
- In a tree, BFS can be visualized by starting at the left-most daughter node of the root node and moving left-to-right. Once the right-most daughter node is visited, move down to the left-most daughter node’s daughter.
Time Complexity
In the following table, V and E refer to the lengths of the vertices and edges sets respectively. In mathematical notation, these values would be referred to by |V| and |E|.
| Graph Representation | Operation | Time Complexity |
|---|---|---|
| Adjacency List | Store Graph | O(V + E) |
| Add Vertex | O(1) | |
| Add Edge | O(1) | |
| Remove Vertex | O(E) | |
| Remove Edge | O(V) | |
| Check Vertex Adjacency | O(V) | |
| Adjacency Matrix | Store Graph | O(V2) |
| Add Vertex | O(V2) | |
| Add Edge | O(1) | |
| Remove Vertex | O(V2) | |
| Remove Edge | O(1) | |
| Check Vertex Adjacency | O(1) | |
| Incidence Matrix | Store Graph | O(V * E) |
| Add Vertex | O(V * E) | |
| Add Edge | O(V * E) | |
| Remove Vertex | O(V * E) | |
| Remove Edge | O(V * E) | |
| Check Vertex Adjacency | O(E) |
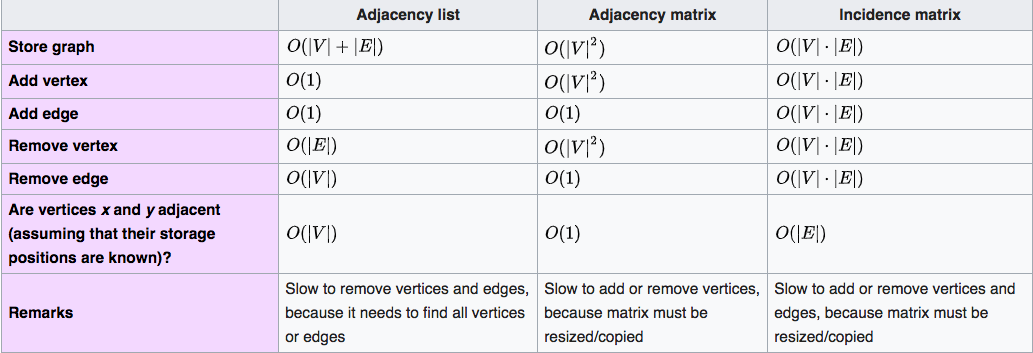
As you can see, different graph representations have different strengths. Make sure to choose the appropriate representation based off which operations you’ll be performing the most!
Practice Questions
Check out Graph Data Structure Interview Questions and Practice Problems by Medium user Coding Freak for a compliation of common graph-related problems.