Day 18: More DP

Introduction

Want to learn more about stacks, click here!

Question 1

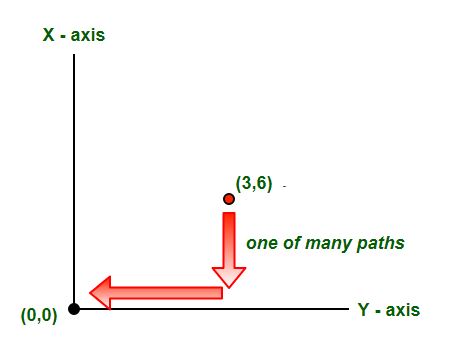
Paths to Origin: Given a point in a standard cartesian (x,y) plane, count the number of different paths you can take to get to the origin,

Input: (3,6)

Output: 84

Constraints:

• CAN ONLY GO DOWN OR RIGHT
• MUST BE RECURSIVE

    int countPaths(int n, int m)
    {
        if (n == 0 || m == 0) return 1;
        return (countPaths(n - 1, m) + countPaths(n, m - 1));
    }

Discussion

This is simple and releated to the way we deal with trees and functions.

Question 1 - V2

Paths to Origin: Given a point in a standard cartesian (x,y) plane, count the number of different paths you can take to get to the origin,

Input: (3, 6)

Output: 84

Constraints:

• MUST BE A DP SOLUTION

    int countPaths(int n, int m)
    {
        int dp[][] = new int[n + 1][m + 1];
     
        for (int i = 0; i <= n; i++)
            dp[i][0] = 1;
        
        for (int j = 0; j <= m; j++)
            dp[0][j] = 1;
     
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= m; j++)
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
     
        return dp[n][m];
    }

Discussion

Here we take the bottom up approach to fill the table pulling from the values we have seen to determine the value where we will go.

Credit: https://www.geeksforgeeks.org/counts-paths-point-reach-origin/

---

Previous:
Day 17: Fun With DP

Next Post:
Day 19: Final Review

return to archives